According to behavioral psychology¹ and specifically research in instructional design, skill development progresses through four stages: (1) acquisition, (2) fluency-building, (3) and generalization.

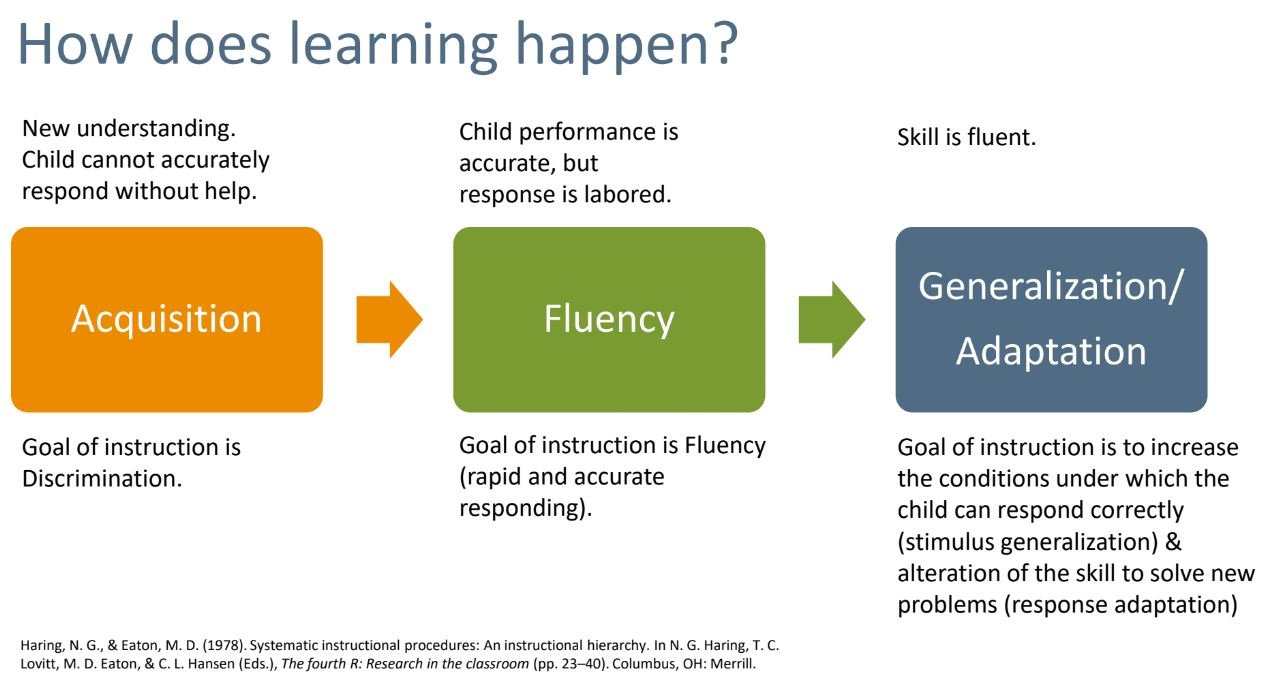
What is Acquisition?

• In the acquisition stage of learning, the student does not yet understand how to correctly respond or what makes one response correct and a different response incorrect.
• Students will often make errors in this stage of learning and may need both antecedent and consequent support to establish correct and independent responding.
• Instructional strategies should focus on sequencing of the task presentation to promote accurate understanding of how and why a given response is correct, modeling, prompting and cuing correct responses in incremental steps, and immediate corrective feedback. The goal is to not allow errors to go undetected and to assist the student to experience a high rate of success while independent performance improves.
• Once a child is accurate and independent, then the student is ready for fluency-building.

What is Fluency-Building?

• A learner in the fluency-building stage of learning is now accurate (e.g., over 90% correct), but is still slow, and requires considerable cognitive resources to complete the task. For example, students solving computations by counting on their fingers or finding a known and counting to solve an unknown may respond correctly, but that responding is so labor-intensive, that the student is not able to think about the problem they are solving, estimate quantity and check their own accuracy as they work, understand the level of precision required in a given context, and plan future problem-solving steps. Fluency-building instruction makes responding easier.
• High-quality fluency-building instruction involves controlled episodes of timed practice with delayed feedback and students trying to beat their last best scores. Fluency is defined as accuracy plus speed² which means it requires a timed dimension. Timed performance is necessary because children are already accurate when they enter the fluency-building stage of instruction (thus, accuracy is no longer a sensitive metric of improvement).^3,4
• Fluent performance yields skills and understanding that are retained over time,⁵ result in faster learning of more complex related skills,⁶ and flexible skill performance.⁷ When students are fluent on a given skill, they are ready for generalization opportunities.

What is Generalization?

• Generalization takes three forms in academic performance—persistence over time (i.e., retention or maintenance), correct skill performance in novel or untrained stimulus conditions (e.g., new tasks like a word problem), and modification of the response to correctly solve problems (e.g., solving a problem using a more efficient method). Generalization is highly related to mathematical flexibility. Effective generalization strategies include
• Independent and repeated opportunities for distributed practice⁸ and mixed cumulative review activities⁵ to promote maintenance.
• Metacognitive (self-regulation) strategies including goal setting and reflection, self-monitoring, and self-instruction, tasks and games that require students to combine different concepts or skills, interleaved task⁹ promote generalization, and deliberately novel but related task presentations to promote correct responding to novel or untrained tasks.
• Sabotaging situations (e.g., a cooking project that requires a 1/2 cup quantity and only 1/8 or 1/4 cups are available to solve), “think aloud” problem solving to practice adapting responses to correctly solve problems.

Selecting what to teach by assessing learners’ skill strengths and areas for improvement is only one of two steps for effective instructional planning. This initial step indicates which skills learners have mastered and not mastered. The second step of instructional planning is to align what to teach with how to teach it. The instructional hierarchy helps teachers connect instructional tactic to student need or stated another way, it gives teachers an evidence-based way to decide how to teach a particular skill (i.e., acquisition, fluency-building, or generalization instruction.^10,11,12